ορισμός της αναγωγικής μεθόδου
ο αφαιρετική μέθοδος ή αφαίρεση Είναι μια από τις πιο χρησιμοποιούμενες μεθόδους για την επίτευξη, λήψη, συμπεράσματα για διάφορα θέματα. Το χαρακτηριστικό γνώρισμα αυτής της επιστημονικής μεθόδου είναι αυτό τα συμπεράσματα ήταν πάντα τυπωμένα στις εγκαταστάσεις, δηλαδή, είναι δυνατόν να συναχθεί το συμπέρασμα των προτάσεων που αποτελούν ένα επιχείρημα, από αυτές και μόνο από αυτές γίνεται.
Αυτή η μέθοδος δεν είναι κάτι που η νεωτερικότητα έφερε μακριά από αυτήν, αλλά είναι μια μέθοδος που ήδη αναφέρθηκε στην κλασική αρχαιότητα από τους Αριστοτέλης.
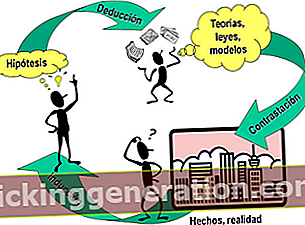
Από την άλλη πλευρά, η έκπτωση, ξεκινά πάντα από μια ερώτηση ή έναν γενικό νόμο για να φτάσουμε στο συγκεκριμένο, δηλαδή, πηγαίνει από το γενικό στο συγκεκριμένο και αυτό είναι που τον αντιμετωπίζει επαγωγική μέθοδος που κινείται στην αντίθετη πλευρά: από το συγκεκριμένο στο γενικό.
Όλοι οι Ισπανοί είναι χαρούμενοι, ο Μιγέλ είναι Ισπανός, οπότε ο Μιγέλ είναι χαρούμενος. Το εκτεθειμένο είναι ένα αυθεντικό αξίωμα της μεθόδου που μας απασχολεί, ωστόσο, είναι σημαντικό να επισημάνουμε ότι όταν οι προτάσεις είναι αληθείς, η συλλογική συλλογιστική θα είναι έγκυρη και επομένως δεν θα υπάρχει τρόπος ότι το συμπέρασμα δεν είναι επίσης αλήθεια.
Εν τω μεταξύ, όσοι επικρίνουν αυτή τη μέθοδο, είναι η περίπτωση του φιλόσοφος Francis Bacon, ένθερμος υπερασπιστής της επαγωγικής μεθόδου, θεωρείτε ότι η μετάβαση από το γενικό στο συγκεκριμένο είναι αυτό που μπορεί αναπόφευκτα να οδηγήσει σε ένα εσφαλμένο συμπέρασμα, ακριβώς λόγω της γενίκευσης στην οποία πραγματοποιείται, θα είναι διαφορετικό όταν ξεκινάμε από συγκεκριμένες ερωτήσεις και μετά φθάνουμε σε ένα γενικό συμπέρασμα.
Ένα άλλο χαρακτηριστικό αυτής της μεθόδου είναι η χρήση διαφορετικών εργαλείων και στοιχείων για την επίδειξη ή την αποσαφήνιση ζητημάτων. Σχέδια, πίνακες γραφικών, συνόψεις, μεταξύ άλλων, που συλλέγουν τις διάφορες προτάσεις καθώς και τις σχέσεις που δημιουργούνται μεταξύ τους και που είναι οι ιδανικοί βοηθοί από αυτή την άποψη.
