ορισμός των τριγωνομετρικών ταυτοτήτων
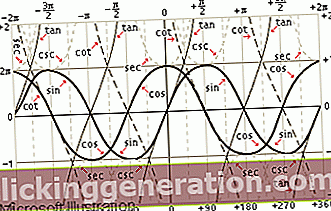 Η έννοια των τριγωνομετρικών ταυτοτήτων είναι μια έννοια που χρησιμοποιείται στον τομέα των μαθηματικών για να αναφέρεται στις μεταβλητές τριγωνομετρικές συναρτήσεις που μπορούν να βρεθούν σε ένα γεωμετρικό σχήμα. Η τριγωνομετρία είναι ο κλάδος των μαθηματικών που ειδικεύεται στην ανάλυση και τη μελέτη των τριγώνων, ειδικά στα σχήματα, τις έννοιες και τις τιμές των διαφορετικών γωνιών που μπορεί να υπάρχουν. Οι τριγωνομετρικές ταυτότητες θα είναι τότε το αποτέλεσμα εκείνων των τιμών που είναι μεταβλητές και πολύ διαφορετικές από τη μία στην άλλη.
Η έννοια των τριγωνομετρικών ταυτοτήτων είναι μια έννοια που χρησιμοποιείται στον τομέα των μαθηματικών για να αναφέρεται στις μεταβλητές τριγωνομετρικές συναρτήσεις που μπορούν να βρεθούν σε ένα γεωμετρικό σχήμα. Η τριγωνομετρία είναι ο κλάδος των μαθηματικών που ειδικεύεται στην ανάλυση και τη μελέτη των τριγώνων, ειδικά στα σχήματα, τις έννοιες και τις τιμές των διαφορετικών γωνιών που μπορεί να υπάρχουν. Οι τριγωνομετρικές ταυτότητες θα είναι τότε το αποτέλεσμα εκείνων των τιμών που είναι μεταβλητές και πολύ διαφορετικές από τη μία στην άλλη.
Όπως με πολλά στοιχεία των μαθηματικών, οι έννοιες υπήρχαν από τα αρχαία χρόνια, όπου οι Έλληνες φιλόσοφοι είχαν ήδη καθιερώσει τις έννοιες των λειτουργιών και των αξιών των γωνιών των γεωμετρικών μορφών. Αυτές οι έννοιες θα βελτιώνονταν μόνο στη νεωτερικότητα, τον δέκατο έβδομο αιώνα, όταν είχαν επισημανθεί αλγεβρικά ότι ήταν σε θέση να εκτελούν κάθε είδους υπολογισμούς μεταξύ των διαφορετικών γωνιών.
Οι τριγωνομετρικές ταυτότητες μπορούν να οριστούν ευρέως ως όλες οι πιθανές μεταβλητές γωνίας που μπορούν να υπάρχουν σε ένα γεωμετρικό σχήμα. Αυτές οι ταυτότητες αντιπροσωπεύονται πάντα από τα ελληνικά γράμματα όπως άλφα, βήτα, ωμέγα κ.λπ. Στοιχεία όπως οι βαθμοί Κελσίου χρησιμοποιούνται επίσης για τον καθορισμό των μεταβλητών κάθε ταυτότητας. Τα πιο γνωστά είναι εκείνα που δημιουργούνται μεταξύ ημιτονοειδούς και συνημίτονου, ημιτονοειδούς και εφαπτομένου, κ.λπ. Οι τριγωνομετρικές ταυτότητες είναι απλουστευμένες μορφές που μας επιτρέπουν να εκτελούμε και να γνωρίζουμε τις διαφορετικές λειτουργίες της τριγωνομετρίας. Όλες αυτές οι ερωτήσεις των μαθηματικών, πιο συγκεκριμένα της τριγωνομετρίας, χρησιμεύουν για την οργάνωση των διαφορετικών υπολογισμών που πρέπει να πραγματοποιούνται από τις συγκεκριμένες λειτουργίες κάθε τύπου δεδομένων. Οι τριγωνομετρικές ταυτότητες είναι πολύ μεταβλητές και επιτρέπουν να έχουν διαφορετικές δυνατότητες να αντιπροσωπεύουν κάθε τριγωνομετρική συνάρτηση (δηλαδή τις τιμές) με ποικίλους και συγκεκριμένους τρόπους σύμφωνα με κάθε περίπτωση.










