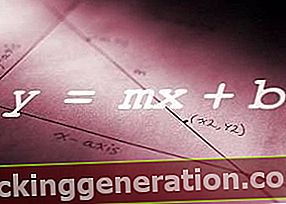ορισμός της άλγεβρας
Η άλγεβρα είναι γνωστή ως ο τομέας των μαθηματικών που είναι υπεύθυνοι για τη διερεύνηση δομών, σχέσεων και ποσοτήτων. Στην άλγεβρα και σε αντίθεση με την αριθμητική που χρησιμοποιεί αριθμούς, αυτά αντικαθίστανται από σύμβολα, για διάφορους λόγους, πρώτον επειδή θα είναι ευκολότερο να διαμορφωθούν γενικοί νόμοι αριθμητικής, για παράδειγμα a + b = b + a, δεύτερος επειδή θα επιτρέπει την αναφορά σε άγνωστους αριθμούς, τη διαμόρφωση εξισώσεων και τη μελέτη του τρόπου επίλυσής τους και τέλος επειδή Τα σύμβολα είναι πιο λειτουργικά κατά τη διαμόρφωση λειτουργικών σχέσεων, συγχωρήστε τον πλεονασμό.
Από την άλλη πλευρά, οι αλγεβρικές δομές είναι ένα σύνολο στοιχείων που έχουν ορισμένες λειτουργικές ιδιότητες, ενώ αυτό που θα καθορίσει τη δομή είναι εκείνες οι λειτουργίες που μπορούν να εκτελεστούν με τα στοιχεία που αποτελούν το εν λόγω σύνολο και τις μαθηματικές ιδιότητες που συνεπάγονται αυτές οι λειτουργίες. Μεταξύ των πιο κοινών αλγεβρικών δομών που μπορούμε να αναφέρουμε: η ομάδα, ο δακτύλιος, το σώμα, το μονοειδές, ο διανυσματικός χώρος, η ενότητα, μεταξύ άλλων.
Όπως είπαμε παραπάνω, Η άλγεβρα χρησιμοποιεί διάφορα σημεία και σύμβολα που φυσικά, στο αλγεβρικό πλαίσιο, θα έχει μια συγκεκριμένη έννοια. Για παράδειγμα, το σύμβολο + εκφράζει την προσθήκη και χρησιμοποιείται για την έκφραση δυαδικών λειτουργιών, τα πρώτα γράμματα του αλφαβήτου που εκφράζουν γνωστές ποσότητες, ενώ τα τελευταία γράμματα χρησιμεύουν, αντίθετα, για αναφορά στα άγνωστα, το γράμμα n είναι γνωστό. να χρησιμοποιείται όταν θέλετε να εκφράσετε οποιαδήποτε ποσότητα και co to k για να αναφέρεται σε σταθερούς όρους, μεταξύ άλλων.
