ορισμός της εξίσωσης
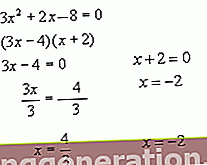Στα μαθηματικά, η ισότητα μεταξύ δύο αλγεβρικών εκφράσεων ονομάζεται εξίσωση, η οποία θα ονομάζεται μέλη της εξίσωσης. Σε εξισώσεις, θα εμφανίζονται σχετικές μέσω μαθηματικών πράξεων, αριθμών και γραμμάτων (άγνωστα).
Τα περισσότερα μαθηματικά προβλήματα βρίσκουν τις συνθήκες που εκφράζονται με τη μορφή μιας ή περισσότερων εξισώσεων.
Εν τω μεταξύ, όταν οποιαδήποτε από τις τιμές των μεταβλητών στην εξίσωση πληροί την ισότητα, αυτή η κατάσταση θα ονομάζεται λύση της εξίσωσης.
Πριν από μια εξίσωση, μπορούν να προκύψουν τα ακόλουθα σενάρια, ότι καμία από τις τιμές της άγνωστης επίτευξης ισότητας, ή αντίθετα, ότι κάθε πιθανή τιμή του άγνωστου την πληροί, στην περίπτωση αυτή θα ήμασταν αντιμέτωποι με αυτό που ονομάζεται ταυτότητες μαθηματικά και όταν δύο μαθηματικές εκφράσεις συμπίπτουν στην ανισότητα, θα καθοριστεί ως ανισότητα.
Υπάρχουν διάφοροι τύποι εξισώσεων, μεταξύ των οποίων, βρίσκουμε τη λειτουργική εξίσωση, η οποία είναι εκείνη στην οποία οι σταθερές και οι μεταβλητές δεν είναι πραγματικοί αριθμοί αλλά συναρτήσεις. Όταν ένας διαφορικός τελεστής εμφανίζεται σε ορισμένα από τα μέλη, ονομάζονται διαφορικές εξισώσεις. Τότε υπάρχει η πολυωνυμική εξίσωση, η οποία θα είναι αυτή που καθιερώνει την ισότητα μεταξύ δύο πολυωνύμων. Από την άλλη πλευρά, οι εξισώσεις πρώτου βαθμού είναι εκείνες στις οποίες η μεταβλητή x δεν αυξάνεται σε καμία ισχύ, με το 1 να είναι εκθετικό της. Εν τω μεταξύ, το χαρακτηριστικό και το διαφορικό χαρακτηριστικό των εξισώσεων που είναι γνωστές ως εξισώσεις δεύτερου βαθμού είναι ότι θα έχουν δύο πιθανές λύσεις σε αυτό.
Αλλά για την αστρονομία, όπου ο όρος λέει επίσης παρόν, μια εξίσωση είναι η διαφορά μεταξύ του τόπου ή της μέσης κίνησης και της πραγματικής ή προφανής που έχει ένα αστέρι.
